Дана тема має широке практичне застосування, тому розглянемо деякі типи розв’язування задач. Нагадаємо, що будь-які побудови виконуються виключно за допомогою циркуля і лінійки.
Приклад 1:
Побудувати трикутник за двома сторонами і кутом між ними.
Дано: Припустимо, аналізований трикутник виглядає так
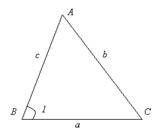
Нехай задані відрізки будуть с і а, а заданий кут буде ∠1
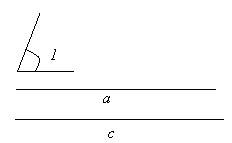
Побудова:
Спочатку слід відкласти кут 1
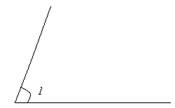
Потім на сторонах даного кута відкладаємо циркулем дві задані сторони: заміряємо циркулем довжину сторони а і поміщаємо вістря циркуля в вершину кута 1, а іншою частиною робимо насічку на стороні кута 1. Аналогічну процедуру проробляємо з стороною с
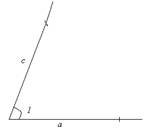
Потім з’єднуємо отримані насічки, і ми отримаємо шуканий трикутник АВС
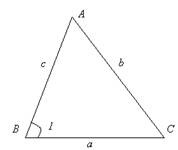
Чи буде цей трикутник рівний передбачуваному? Буде, адже елементи отриманого трикутника (дві сторони і кут між ними) відповідно рівні двом сторонам і куту між ними, даними в умові. Тому за першою властивістю рівності трикутників – ΔABC – шуканий.
Побудовe виконано.
Приклад 2
Відкласти від даного променя кут, рівний даному. Заданий кут А і промінь ОМ. Побудувати ∠МОЕ = ∠А.
Побудова:
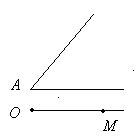
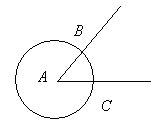
- Побудувати коло Окр (А, r = AB). Точки В і С – є точками перетину зі сторонами кута А
- Побудувати коло Окр (D, r = CB). Точки E і M – є точками перетину зі сторонами кута А
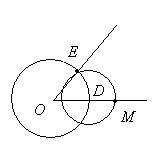
- Кут МОЕ – шуканий, так як ΔАВС = ΔОВЕ.
Побудову виконано.
Домашнє завдання: закріпити тему “Побудова трикутника за трьома сторонами” завданнями відповідного розділу у вашому підручнику.







