Всі ви пам’ятаєте, що таке прямий кут. В математиці і в житті прямі кути зустрічаються досить часто. Якщо ви розглянете квадрат, то помітите, що сторони квадрата перетинаються під прямим кутом. Якщо розглянути залізничну колію, можна побачити, що рейки і шпали розташовані під прямим кутом один до одного; стіни будинку найчастіше роблять під прямим кутом до фундаменту і т. д.
Перпендикулярні прямі
У математиці є спеціальне позначення для прямих, які перетинаються під прямим кутом. Такі прямі називають перпендикулярними. Позначають символом: a⟂b (a перпендикулярна b).
Перпендикулярними бувають і відрізки.
Відрізки називаються перпендикулярними, коли прямі, які їх містять, перпендикулярні.
Дане твердження легко зрозуміти, згадавши квадрат – прямі, що містять сусідні сторони квадрата, перпендикулярні, значить, і відрізки (сторони) перпендикулярні.
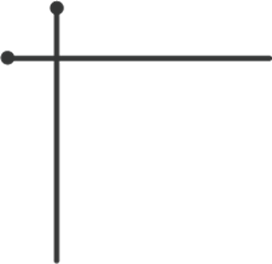
Відрізки, показані на малюнку, також перпендикулярні. Чому?

Якщо ці відрізки продовжити до прямих, то прямі перетнуться під прямим кутом. Значить, якщо прямі перпендикулярні, то і відрізки теж перпендикулярні, хоча і не перетинаються.
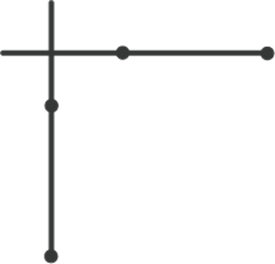
Промені називають перпендикулярними, якщо прямі, що містять ці промені, перпендикулярні.
Побудова перпендикулярних прямих
Є декілька способів:
- За допомогою косинця, так як дві його сторони утворюють прямий кут.
- За допомогою транспортира – відзначити кут 90° і провести прямі, які його утворюють.
- За допомогою циркуля і лінійки (з цим способом ви познайомитеся в 7 класі на уроці геометрії).
Особливість перпендикулярних прямих
Чому саме такий тип прямих виділили в окремий клас? Чому не говоримо окремо про прямі, які просто перетинаються одині з одними під якимось іншим кутом, наприклад 60°?
Відповідь наступна: при перетині прямих у нас утворюються кути, найчастіше вони не рівні.
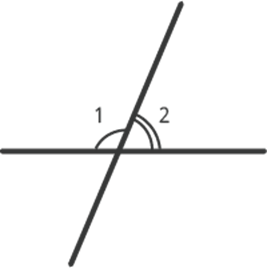
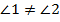
Але якщо ми говоримо про перпендикулярні прямі, то це єдиний випадок, коли утворилися кути рівні між собою – всі вони прямі.
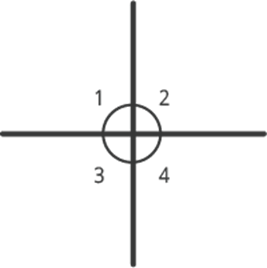
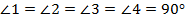
Саме тому ці прямі і виділили, тим більше в житті ми з ними стикаємося частіше, ніж з прямими, які перетинаються під будь-яким іншим кутом.
Запитання, пов’язані з перпендикулярними прямими
На деякій прямій позначили точку.

Скільки прямих можна провести через цю точку так, щоб вони були перпендикулярні заданій прямій?
Відповідь: тільки одну. Потрібно з допомогою кутника і провести відповідну пряму.

- Дана пряма і точка поза нею.

Скільки прямих проходять через цю точку так, що вони перпендикулярні заданій прямій?
Відповідь: одна пряма. Знову ж таки, це можна зробити за допомогою кутника.

Паралельні прямі
Ми говорили про прямі, які перетинаються. Але буває ж так, що прямі не перетинаються. З цим ми стикаємося і в житті – у лижників під час спуску права лижня і ліва не перетинаються; або доріжки в басейні – вони також не перетинаються; або залізнична колія – рейки не перетинаються. Для непересічних прямих також є спеціальна назва.
Прямі на площині, які не перетинаються, називаються паралельними.
Дуже важливо тут додати «на площині», тому що, коли в 10 класі ви зіткнетеся з прямими в просторі, виявиться, що є прямі, які не перетинаються, але і не є паралельними. Зараз же мова йде про площину, і на площині є два випадки: прямі або перетинаються, або паралельні (не перетинаються).
Паралельні прямі позначають символом: a II b (a паралельна b).
За аналогією з перпендикулярними відрізками і променями є також визначення паралельних відрізків і променів.
Відрізки називаються паралельними, якщо вони лежать на паралельних прямих.
Промені називаються паралельними, якщо вони лежать на паралельних прямих.

Таким чином, коли ми говоримо про доріжки в басейні, мова йде скоріше про паралельні відрізки (доріжки обмежені), ніж про прямі.
Запитання, пов’язані з паралельними прямими
Чи вірно, що якщо два відрізки не перетинаються, то вони паралельні?
Відповідь: ні, не вірно. Наведемо приклад.

Ці два відрізки не перетинаються, але вони не є паралельними, так як прямі, що містять їх, перетинаються. Аналогічно з променями – якщо промені не перетинаються, вони не обов’язково паралельні.
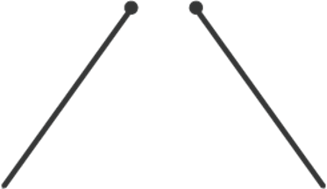
Можна згадати приклади, які ми наводили на початку уроку – промені і відрізки не перетиналися, але і не були паралельними, тому що вони перпендикулярні.
Побудова паралельних прямих
Розглянемо конструкцію, що складається з трьох прямих a, b і c, де a ⊥ b, c ⊥ b.
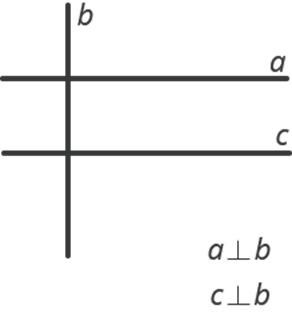
Тоді, що ми можемо сказати про прямі а і с? Судячи по картинці, вони паралельні. Довести ми цього поки не можемо, але тим не менше це якраз і є спосіб побудови паралельних прямих. Тобто паралельні прямі будуються через перпендикулярність – спочатку проводять пряму, перпендикулярну заданій, (в нашому випадку a ⊥ b), а потім проводять пряму, перпендикулярну другій (в нашому випадку c ⊥ b).
Відзначимо, що з зазначених фактів випливає паралельність протилежних сторін квадрата і прямокутника – вони перпендикулярні одній і тій же стороні.
Є ще один цікавий факт. Проведемо дві паралельні прямі, а також третю пряму, яка паралельна першій, тобто a II b, a II c.
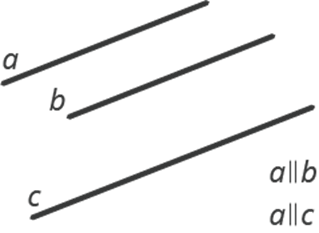
Судячи по малюнку b II c теж. Цей факт вірний, але, знову ж таки, доводити ми його будемо в 7 класі.
Висновок: на цьому уроці ми познайомилися з поняттями паралельних і перпендикулярних прямих; ми з’ясували, які відрізки і промені називають перпендикулярними, а які – паралельними; дізналися, як будуються перпендикулярні та паралельні прямі.
Домашнє завдання: Збірник. Мерзляк 220-224 (І варіант)